TVM Learning (4)-End to End Model Execution

E2E Model Integration

我们以下图中的 MLP 网络为例，这是一个两层全连接网络，并且省略了最后的 Softmax 层。

img

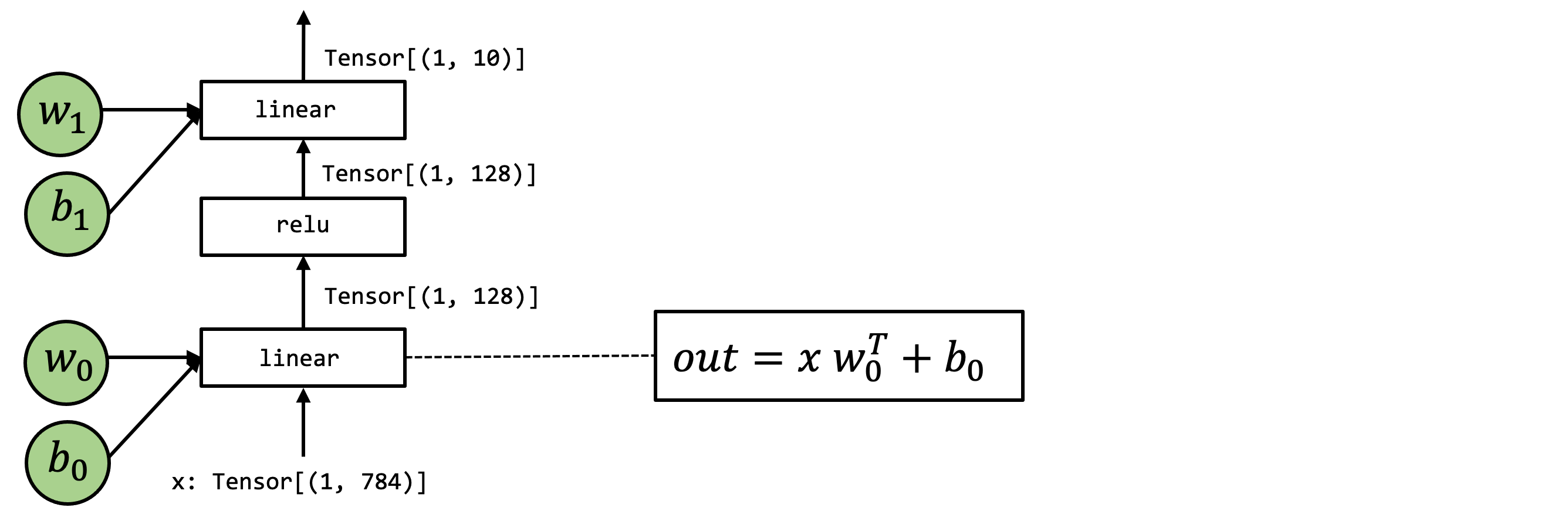
利用高级Numpy的实现如下

1
2
3
4
5
def numpy_mlp(data, w0, b0, w1, b1):
    lv0 = data @ w0.T + b0
    lv1 = np.maximum(lv0, 0)
    lv2 = lv1 @ w1.T + b1
    return lv2

为了方便说明底层计算过程，用 Low-level Numpy 进行重写后如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def lnumpy_linear0(X: np.ndarray, W: np.ndarray, B: np.ndarray, Z: np.ndarray):
    Y = np.empty((1, 128), dtype="float32")
    for i in range(1):
        for j in range(128):
            for k in range(784):
                if k == 0:
                    Y[i, j] = 0
                Y[i, j] = Y[i, j] + X[i, k] * W[j, k]

    for i in range(1):
        for j in range(128):
            Z[i, j] = Y[i, j] + B[j]


def lnumpy_relu0(X: np.ndarray, Y: np.ndarray):
     for i in range(1):
        for j in range(128):
            Y[i, j] = np.maximum(X[i, j], 0)

def lnumpy_linear1(X: np.ndarray, W: np.ndarray, B: np.ndarray, Z: np.ndarray):
    Y = np.empty((1, 10), dtype="float32")
    for i in range(1):
        for j in range(10):
            for k in range(128):
                if k == 0:
                    Y[i, j] = 0
                Y[i, j] = Y[i, j] + X[i, k] * W[j, k]

    for i in range(1):
        for j in range(10):
            Z[i, j] = Y[i, j] + B[j]


def lnumpy_mlp(data, w0, b0, w1, b1):
    lv0 = np.empty((1, 128), dtype="float32")
    lnumpy_linear0(data, w0, b0, lv0)

    lv1 = np.empty((1, 128), dtype="float32")
    lnumpy_relu0(lv0, lv1)

    out = np.empty((1, 10), dtype="float32")
    lnumpy_linear1(lv1, w1, b1, out)
    return out

Constructing an E2E IRModule in TVMScript

同样可以用 TVMScript 构建这个网络的 IRModule，只不过这次除了要用 Primitive Tensor Function (@T.prim_function) 还要用 Relax Function (@R.function) 来抽象神经网络的计算过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
@tvm.script.ir_module
class MyModule: 
    @T.prim_func
    def relu0(X: T.Buffer((1, 128), "float32"), 
              Y: T.Buffer((1, 128), "float32")):
        # function attr dict
        T.func_attr({"global_symbol": "relu0", "tir.noalias": True})
        for i, j in T.grid(1, 128):
            with T.block("Y"):
                vi, vj = T.axis.remap("SS", [i, j])
                Y[vi, vj] = T.max(X[vi, vj], T.float32(0))

    @T.prim_func
    def linear0(X: T.Buffer((1, 784), "float32"), 
                W: T.Buffer((128, 784), "float32"), 
                B: T.Buffer((128,), "float32"), 
                Z: T.Buffer((1, 128), "float32")):
        T.func_attr({"global_symbol": "linear0", "tir.noalias": True})
        Y = T.alloc_buffer((1, 128), "float32")
        for i, j, k in T.grid(1, 128, 784):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
  
        for i, j in T.grid(1, 128):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                Z[vi, vj] =  Y[vi, vj] + B[vj]

    @T.prim_func
    def linear1(X: T.Buffer((1, 128), "float32"), 
                W: T.Buffer((10, 128), "float32"), 
                B: T.Buffer((10,), "float32"), 
                Z: T.Buffer((1, 10), "float32")):
        T.func_attr({"global_symbol": "linear1", "tir.noalias": True})
        Y = T.alloc_buffer((1, 10), "float32")
        for i, j, k in T.grid(1, 10, 128):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
  
        for i, j in T.grid(1, 10):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                Z[vi, vj] = Y[vi, vj] + B[vj]

    @R.function
    def main(x: R.Tensor((1, 784), "float32"), 
             w0: R.Tensor((128, 784), "float32"), 
             b0: R.Tensor((128,), "float32"), 
             w1: R.Tensor((10, 128), "float32"), 
             b1: R.Tensor((10,), "float32")):
        with R.dataflow():
            cls = MyModule
            lv0 = R.call_tir(cls.linear0, (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            lv1 = R.call_tir(cls.relu0, (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            out = R.call_tir(cls.linear1, (lv1, w1, b1), out_sinfo=R.Tensor((1, 10), dtype="float32"))
            R.output(out)
        return out

Computational Graph View

该网络的计算图如下，计算图通常具有以下性质：

  • 框的每个输入边对应于操作的输入；
  • 每个出边对应于操作的输出；
  • 可以任意调整操作的顺序，只要保证边的拓扑排序（Topological Order）没有改变。

拓扑排序是针对有向无环图 (DAG) 的一种排序算法，它将图中的节点排成一个线性序列，满足以下条件：

  • 对于图中的任意一条边 (u, v)，节点 u 在排序中都出现在节点 v 之前。

dag

进行拓扑排序较常用的方法：

  1. 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
  2. 从图中删除该顶点和所有以它为起点的有向边。
  3. 重复 1 和 2 直到当前的 DAG 图为空或 当前图中不存在无前驱的顶点为止 。后一种情况说明有向图中必然存在环。

topo sort

Computational Graph View

R.call_tir

R.call_tir 正如名字一样调用一个 T.prim_func 并返回计算结果。它的行为用Numpy表示如下，先根据 shape和 dtype开辟输出数据的内存空间，然后调用函数，最后返回输出结果。R.call_tir函数的输入是这种形式的原因是 T.prim_func函数的输入需要我们先为输出结果开辟内存，称为 目标传递 (destination passing) 。

1
2
3
4
def lnumpy_call_tir(prim_func, inputs, shape, dtype):
    res = np.empty(shape, dtype=dtype)
    prim_func(*inputs, res)
    return res

为了让程序执行具有计算图的性质，我们采用这种方式进行调用

1
2
3
4
5
def lnumpy_mlp_with_call_tir(data, w0, b0, w1, b1):
    lv0 = lnumpy_call_tir(lnumpy_linear0, (data, w0, b0), (1, 128), dtype="float32")
    lv1 = lnumpy_call_tir(lnumpy_relu0, (lv0, ), (1, 128), dtype="float32")
    out = lnumpy_call_tir(lnumpy_linear1, (lv1, w1, b1), (1, 10), dtype="float32")
    return out

Dataflow Block

理想情况下，计算图中的操作应为 side-effect free，即一个函数只从其输入中读取并通过其输出返回结果，不会改变程序的其他部分（例如递增全局计数器）。如果要引入包含 side-effect 的操作，就需要定义多个dataflow block，在他们之外或者之间进行操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
@R.function
def main(x: Tensor((1, 784), "float32"), 
         w0: Tensor((128, 784), "float32"), 
         b0: Tensor((128,), "float32"), 
         w1: Tensor((10, 128), "float32"), 
         b1: Tensor((10,), "float32")):

    with R.dataflow():
        lv0 = R.call_tir(cls.linear0, (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
        gv0 = R.call_tir(cls.relu0, (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
        R.output(gv0)

    gv1 = R.alloc_tensor((1, 128), dtype="float32")  # side-effect operation

    with R.dataflow():
        out = R.call_tir(cls.linear1, (gv0, gv1, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
        R.output(out)
    return out

Build and Run the Model

该网络对应的TensorIR如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
@I.ir_module
class Module:
    @T.prim_func
    def linear0(
        X: T.Buffer((1, 784), "float32"),
        W: T.Buffer((128, 784), "float32"),
        B: T.Buffer((128,), "float32"),
        Z: T.Buffer((1, 128), "float32"),
    ):
        T.func_attr({"global_symbol": "linear0", "tir.noalias": T.bool(True)})
        # with T.block("root"):
        Y = T.alloc_buffer((1, 128))
        for i, j, k in T.grid(1, 128, 784):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                T.reads(X[vi, vk], W[vj, vk])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
        for i, j in T.grid(1, 128):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj], B[vj])
                T.writes(Z[vi, vj])
                Z[vi, vj] = Y[vi, vj] + B[vj]

    @T.prim_func
    def linear1(
        X: T.Buffer((1, 128), "float32"),
        W: T.Buffer((10, 128), "float32"),
        B: T.Buffer((10,), "float32"),
        Z: T.Buffer((1, 10), "float32"),
    ):
        T.func_attr({"global_symbol": "linear1", "tir.noalias": T.bool(True)})
        # with T.block("root"):
        Y = T.alloc_buffer((1, 10))
        for i, j, k in T.grid(1, 10, 128):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                T.reads(X[vi, vk], W[vj, vk])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
        for i, j in T.grid(1, 10):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj], B[vj])
                T.writes(Z[vi, vj])
                Z[vi, vj] = Y[vi, vj] + B[vj]

    @T.prim_func
    def relu0(X: T.Buffer((1, 128), "float32"), Y: T.Buffer((1, 128), "float32")):
        T.func_attr({"global_symbol": "relu0", "tir.noalias": T.bool(True)})
        # with T.block("root"):
        for i, j in T.grid(1, 128):
            with T.block("Y"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(X[vi, vj])
                T.writes(Y[vi, vj])
                Y[vi, vj] = T.max(X[vi, vj], T.float32(0))

    @R.function
    def main(
        x: R.Tensor((1, 784), dtype="float32"),
        w0: R.Tensor((128, 784), dtype="float32"),
        b0: R.Tensor((128,), dtype="float32"),
        w1: R.Tensor((10, 128), dtype="float32"),
        b1: R.Tensor((10,), dtype="float32"),
    ) -> R.Tensor((1, 10), dtype="float32"):
        cls = Module
        with R.dataflow():
            lv0 = R.call_tir(cls.linear0, (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            lv1 = R.call_tir(cls.relu0, (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            out = R.call_tir(cls.linear1, (lv1, w1, b1), out_sinfo=R.Tensor((1, 10), dtype="float32"))
            R.output(out)
        return out

我们可以通过下面方式来构造 virtual machine. relax.build返回一个 tvm.relax.Executable对象，然后就可以在指定的硬件上创建virtual machine 来执行计算图。

1
2
3
4
5
6
7
8
ex = relax.build(MyModule, target="llvm")
vm = relax.VirtualMachine(ex, tvm.cpu())

nd_res = vm["main"](data_nd, 
                    nd_params["w0"],
                    nd_params["b0"],
                    nd_params["w1"],
                    nd_params["b1"])

Integrate Existing Libraries in the Environment

除了用 T.prim_func构造RelaxIR，我们也可以从现有的深度学习库的函数来构造。

这是通过 R.call_dps_packed来完成的，它用于调用一个目标传递风格 (Destination-Passing Style) 的打包函数 (Packed Function)，并返回输出结果。

  • 目标传递风格 (Destination-Passing Style): 目标传递风格是一种函数调用方式，其中函数的输出参数作为函数参数传递给函数。
  • 打包函数 (Packed Function): 打包函数是一种函数，其输入参数和输出参数都被打包成一个结构体。
  • 纯函数 (Pure Function): 纯函数是指不产生副作用的函数，即函数的执行结果只依赖于输入参数，并且不会修改任何全局状态。

示例：

1
R.call_dps_packed("env.linear", (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))

函数参数：

  • func: 可以是字符串或表达式，表示目标传递风格的函数。如果 func 是字符串，它将被转换为 ExternFunc 对象。
  • args: 表达式，表示输入参数。如果 args 是单个表达式，它将被包装成一个 RxTuple 对象。
  • out_sinfo: 可以是 TensorStructInfo 对象或 TensorStructInfo 对象列表，表示 call_dps_packed 函数输出的结构信息。每个 TensorStructInfo 对象表示一个返回的张量的结构信息。

函数返回值：

  • ret: Call 对象，表示 call_dps_packed 操作符的调用节点。

Registering Runtime Function

为了能够执行调用外部函数的代码，我们需要注册相应的函数。下面这段代码注册了两个自定义函数，分别用于实现线性层和 ReLU 激活函数。

  1. @tvm.register_func("env.linear", override=True):
    • 使用 @tvm.register_func 装饰器将 torch_linear 函数注册为名为 "env.linear" 的 TVM 函数。
    • override=True 表示如果已经存在同名函数，则覆盖它。
  2. torch_linear(x: tvm.nd.NDArray, w: tvm.nd.NDArray, b: tvm.nd.NDArray, out: tvm.nd.NDArray):
    • 该函数接受四个参数：
      • x: 输入张量。
      • w: 权重张量。
      • b: 偏置张量。
      • out: 输出张量。
    • 函数内部：
      • 使用 torch.from_dlpack 将 TVM 的 NDArray 对象转换为 PyTorch 的 Tensor 对象。
      • 使用 PyTorch 的 torch.mm 函数进行矩阵乘法，将 x 和 w 的转置相乘，并将结果写入 out。
      • 使用 PyTorch 的 torch.add 函数将 b 加到 out 上。
  3. @tvm.register_func("env.relu", override=True):
    • 使用 @tvm.register_func 装饰器将 lnumpy_relu 函数注册为名为 "env.relu" 的 TVM 函数。
    • override=True 表示如果已经存在同名函数，则覆盖它。
  4. lnumpy_relu(x: tvm.nd.NDArray, out: tvm.nd.NDArray):
    • 该函数接受两个参数：
      • x: 输入张量。
      • out: 输出张量。
    • 函数内部：
      • 使用 torch.from_dlpack 将 TVM 的 NDArray 对象转换为 PyTorch 的 Tensor 对象。
      • 使用 PyTorch 的 torch.maximum 函数计算 x 和 0 之间的最大值，并将结果写入 out。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
@tvm.register_func("env.linear", override=True)
def torch_linear(x: tvm.nd.NDArray, 
                 w: tvm.nd.NDArray, 
                 b: tvm.nd.NDArray, 
                 out: tvm.nd.NDArray):
    x_torch = torch.from_dlpack(x)
    w_torch = torch.from_dlpack(w)
    b_torch = torch.from_dlpack(b)
    out_torch = torch.from_dlpack(out)
    torch.mm(x_torch, w_torch.T, out=out_torch)
    torch.add(out_torch, b_torch, out=out_torch)

@tvm.register_func("env.relu", override=True)
def lnumpy_relu(x: tvm.nd.NDArray, 
                out: tvm.nd.NDArray):
    x_torch = torch.from_dlpack(x)
    out_torch = torch.from_dlpack(out)
    torch.maximum(x_torch, torch.Tensor([0.0]), out=out_torch)

然后我们就可以创建IRModule并通过上一节所说方法去 build and run.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
@tvm.script.ir_module
class MyModuleWithExternCall:
    @R.function
    def main(x: R.Tensor((1, 784), "float32"), 
             w0: R.Tensor((128, 784), "float32"), 
             b0: R.Tensor((128,), "float32"), 
             w1: R.Tensor((10, 128), "float32"), 
             b1: R.Tensor((10,), "float32")):
        # block 0
        with R.dataflow():
            lv0 = R.call_dps_packed("env.linear", (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            lv1 = R.call_dps_packed("env.relu", (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            out = R.call_dps_packed("env.linear", (lv1, w1, b1), out_sinfo=R.Tensor((1, 10), dtype="float32"))
            R.output(out)
        return out

ex = relax.build(MyModuleWithExternCall, target="llvm")
vm = relax.VirtualMachine(ex, tvm.cpu())

Mixing TensorIR Code and Libraries

我们可以混合使用T.prim_func和 注册的 runtime 函数来创建 RelaxIR. 以下代码展示了一个例子，其中 linear0 仍在 TensorIR 中实现，而其他函数则被重定向到库函数中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
@tvm.script.ir_module
class MyModuleMixture: 
    @T.prim_func
    def linear0(X: T.Buffer((1, 784), "float32"), 
                W: T.Buffer((128, 784), "float32"), 
                B: T.Buffer((128,), "float32"), 
                Z: T.Buffer((1, 128), "float32")):
        T.func_attr({"global_symbol": "linear0", "tir.noalias": True})
        Y = T.alloc_buffer((1, 128), "float32")
        for i, j, k in T.grid(1, 128, 784):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
  
        for i, j in T.grid(1, 128):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                Z[vi, vj] =  Y[vi, vj] + B[vj]

    @R.function
    def main(x: R.Tensor((1, 784), "float32"), 
             w0: R.Tensor((128, 784), "float32"), 
             b0: R.Tensor((128,), "float32"), 
             w1: R.Tensor((10, 128), "float32"), 
             b1: R.Tensor((10,), "float32")):
        with R.dataflow():
            cls = MyModuleMixture
            lv0 = R.call_tir(cls.linear0, (x, w0, b0), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            lv1 = R.call_dps_packed("env.relu", (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            out = R.call_dps_packed("env.linear", (lv1, w1, b1), out_sinfo=R.Tensor((1, 10), dtype="float32"))
            R.output(out)
        return out

Bind Parameters to IRModule

之前都是通过显示传递参数给 vm["main"]函数来调用，我们也可以将参数当作常熟与IRModule进行绑定。

metadata["relax.expr.Constant"]对应的是存储常量的隐式字典（虽然没有显示在脚本中，但仍是 IRModule 的一部分）。构建了转换后的 IRModule，现在只需输入数据就可以调用函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
MyModuleWithParams = relax.transform.BindParams("main", nd_params)(MyModuleMixture)
MyModuleWithParams.show()

#-------------------------------------
@I.ir_module
class Module:
    @T.prim_func
    def linear0(X: T.Buffer((1, 784), "float32"), W: T.Buffer((128, 784), "float32"), B: T.Buffer((128,), "float32"), Z: T.Buffer((1, 128), "float32")):
        T.func_attr({"tir.noalias": T.bool(True)})
        # with T.block("root"):
        Y = T.alloc_buffer((1, 128))
        for i, j, k in T.grid(1, 128, 784):
            with T.block("Y"):
                vi, vj, vk = T.axis.remap("SSR", [i, j, k])
                T.reads(X[vi, vk], W[vj, vk])
                T.writes(Y[vi, vj])
                with T.init():
                    Y[vi, vj] = T.float32(0.0)
                Y[vi, vj] = Y[vi, vj] + X[vi, vk] * W[vj, vk]
        for i, j in T.grid(1, 128):
            with T.block("Z"):
                vi, vj = T.axis.remap("SS", [i, j])
                T.reads(Y[vi, vj], B[vj])
                T.writes(Z[vi, vj])
                Z[vi, vj] = Y[vi, vj] + B[vj]

    @R.function
    def main(x: R.Tensor((1, 784), dtype="float32")) -> R.Tensor((1, 10), dtype="float32"):
        cls = Module
        with R.dataflow():
            lv0 = R.call_tir(cls.linear0, (x, metadata["relax.expr.Constant"][0], metadata["relax.expr.Constant"][1]), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            lv1 = R.call_dps_packed("env.relu", (lv0,), out_sinfo=R.Tensor((1, 128), dtype="float32"))
            out = R.call_dps_packed("env.linear", (lv1, metadata["relax.expr.Constant"][2], metadata["relax.expr.Constant"][3]), out_sinfo=R.Tensor((1, 10), dtype="float32"))
            R.output(out)
        return out
TVM
#TVM learning
TVM Learning (4)-End to End Model Execution
https://darkenstar.github.io/2024/08/18/chapter3/
Author
ANNIHILATE_RAY
Posted on
August 18, 2024
Licensed under