TVM Learning (2)-Tensor Program Abstraction Case Study-TensorIR

Primitive Tensor Function

机器学习编译的过程可以被看作张量函数之间的变换。一个典型的机器学习模型的执行包含许多步将输入张量之间转化为最终预测的计算步骤，其中的每一步都被称为元张量函数 (Primitive Tensor Function)

通常来说，一个典型的元张量函数实现的抽象包含了以下成分：存储数据的多维数组，驱动张量计算的循环嵌套以及计算部分本身的语句。下图以上一篇中的向量加法为例子进行了分解。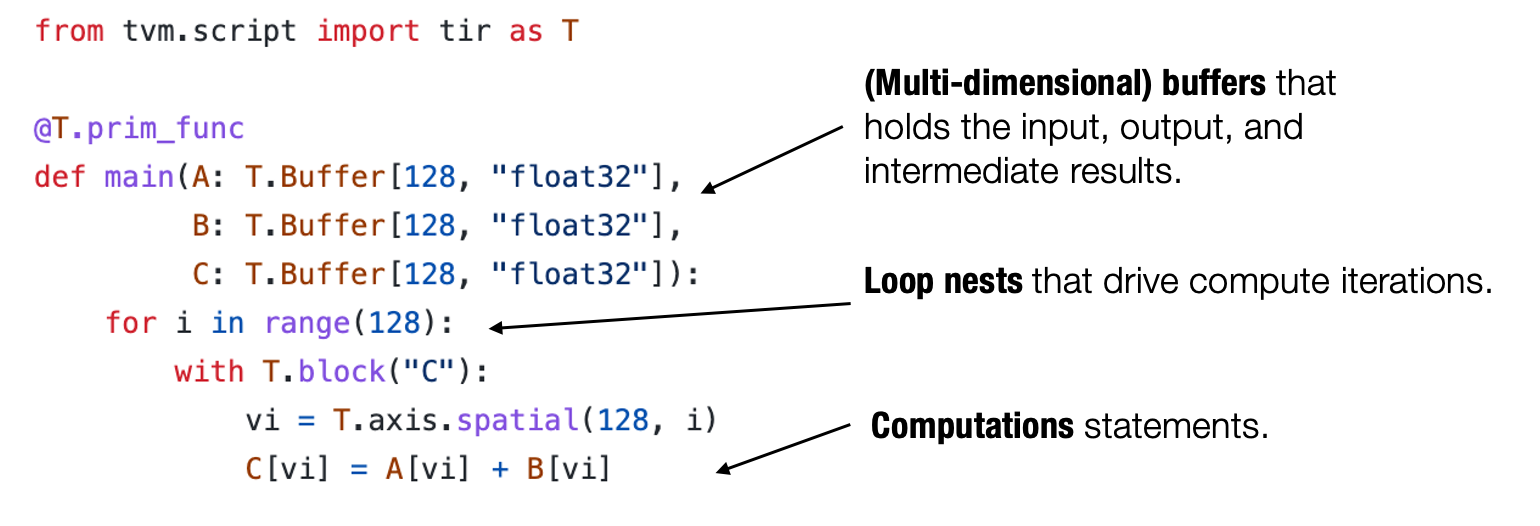
Tensor Function Elements

我们称这类抽象为张量程序抽象(Tensor Program Abstraction). 张量程序抽象的一个重要性质是，他们能够被一系列有效的程序变换所改变。例如，我们能够通过一组变换操作（如循环拆分、并行和向量化）将下图左侧的一个初始循环程序变换为右侧的程序。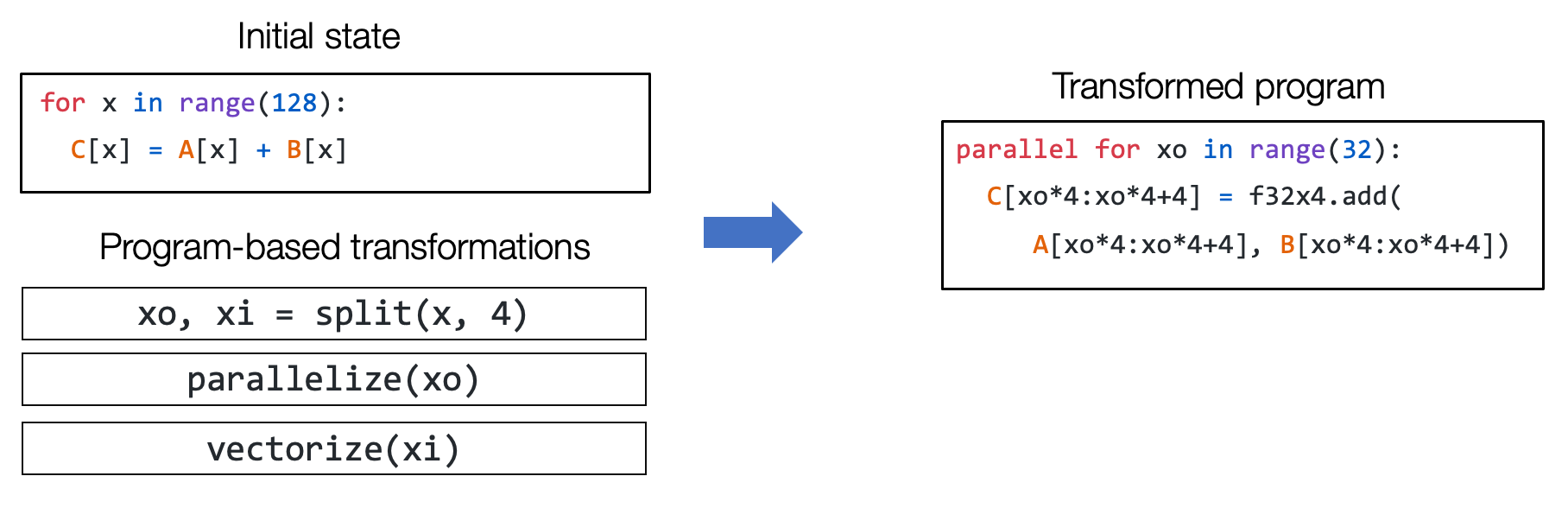
Tensor Function Transforms

Learning one Tensor Program Abstraction – TensorIR

我们对于神经网络的一个基本的 Linear+ReLU 层可以用以下的数学公式表示

$Y_{ij} = \sum_k A_{ik} B_{kj}$
$C_{ij} = \mathbb{ReLU}(Y_{ij}) = \mathbb{max}(Y_{ij}, 0)$

其Numpy实现如下，下面的代码直接调用了Numpy的高级API，看起来非常简洁。

dtype = "float32"
a_np = np.random.rand(128, 128).astype(dtype)
b_np = np.random.rand(128, 128).astype(dtype)
# a @ b is equivalent to np.matmul(a, b)
c_mm_relu = np.maximum(a_np @ b_np, 0)

我们可以将上述程序改写成Low-level Numpy，意味着对于复杂的计算我们使用循环进行表示，并且写出开辟数组空间的过程。

def lnumpy_mm_relu(A: np.ndarray, B: np.ndarray, C: np.ndarray):
    Y = np.empty((128, 128), dtype="float32")
    for i in range(128):
        for j in range(128):
            for k in range(128):
                if k == 0:
                    Y[i, j] = 0
                Y[i, j] = Y[i, j] + A[i, k] * B[k, j]
    for i in range(128):
        for j in range(128):
            C[i, j] = max(Y[i, j], 0)

该函数执行以下操作：

矩阵乘法： 将两个矩阵 A 和 B 相乘，并将结果存储在 Y 中。
ReLU 激活： 将 ReLU 激活函数应用于 Y 的元素，并将结果存储在 C 中。

可以用以下代码来检查上述实现的正确性：

1
2
3

c_np = np.empty((128, 128), dtype=dtype)
lnumpy_mm_relu(a_np, b_np, c_np)
np.testing.assert_allclose(c_mm_relu, c_np, rtol=1e-5)

示例 numpy 代码包含了实际过程中实现这些计算时可能会用到的所有元素，用Numpy函数内部工作机制 (Under the Hood) 实现了MM-ReLU。

开辟多维数组空间。
循环遍历数组的维度。
计算在循环内执行。

我们也可以用上一节的TensorIR来实现，TVMScript 是嵌入在 Python AST 中的领域特定语言的 Dialect, 它本质上是 Python 的一个子集，但添加了一些特定于 TVM 的扩展，例如用于描述计算图的特殊语法和语义。

Dialect 通常指一种语言的变体或子集，它与原始语言共享大部分语法和语义，但也有一些独特的特征。

抽象语法树 (AST) 是源代码的树状表示形式。它将代码的结构以一种层次化的方式呈现，每个节点代表代码中的一个语法元素，例如变量、运算符、函数调用等。

@tvm.script.ir_module
class MyModule:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], 
                B: T.Buffer[(128, 128), "float32"], 
                C: T.Buffer[(128, 128), "float32"]):
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        Y = T.alloc_buffer((128, 128), dtype="float32")
        for i, j, k in T.grid(128, 128, 128):
            with T.block("Y"):
                vi = T.axis.spatial(128, i)
                vj = T.axis.spatial(128, j)
                vk = T.axis.reduce(128, k)
                with T.init():
                    Y[vi, vj] = T.float32(0)
                Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
        for i, j in T.grid(128, 128):
            with T.block("C"):
                vi = T.axis.spatial(128, i)
                vj = T.axis.spatial(128, j)   
                C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

上述 TensorIR 程序的一个示例实例涵盖了大部分内容，包括

参数和中间临时内存中的缓冲区声明。
For 循环迭代。
Block 和 Block Axis属性。

Transformation

TVM 的 tvm.tir.Schedule 提供了一系列用于调度和优化计算图的变换函数。这些函数允许用户灵活地调整计算顺序、内存访问模式和并行化策略，以提高模型的性能。

我们可以用以下函数获得计算块和其对应的循环

1 2	`block_Y = sch.get_block("Y", func_name="mm_relu") i, j, k = sch.get_loops(block_Y)`

我们可以使用 split函数将一个循环拆成多个循环，用 reorder函数交换循环的顺序，用 reverse_compute_at 函数移动计算块所在的循环，用 decompose_reduction函数将初始化和归约操作分开。

j0, j1 = sch.split(j, factors=[None, 4])
sch.reorder(j0, k, j1)
block_C = sch.get_block("C", "mm_relu")
sch.reverse_compute_at(block_C, j0)
block_Y = sch.get_block("Y", "mm_relu")
sch.decompose_reduction(block_Y, k)
sch.mod.show()
# Output
@tvm.script.ir_module
class Module:
    @T.prim_func
    def mm_relu(A: T.Buffer[(128, 128), "float32"], B: T.Buffer[(128, 128), "float32"], C: T.Buffer[(128, 128), "float32"]) -> None:
        # function attr dict
        T.func_attr({"global_symbol": "mm_relu", "tir.noalias": True})
        # body
        # with T.block("root")
        Y = T.alloc_buffer([128, 128], dtype="float32")
        for i, j_0 in T.grid(128, 32):
            for j_1_init in T.serial(4):
                with T.block("Y_init"):
                    vi = T.axis.spatial(128, i)
                    vj = T.axis.spatial(128, j_0 * 4 + j_1_init)
                    T.reads()
                    T.writes(Y[vi, vj])
                    Y[vi, vj] = T.float32(0)
            for k, j_1 in T.grid(128, 4):
                with T.block("Y_update"):
                    vi = T.axis.spatial(128, i)
                    vj = T.axis.spatial(128, j_0 * 4 + j_1)
                    vk = T.axis.reduce(128, k)
                    T.reads(Y[vi, vj], A[vi, vk], B[vk, vj])
                    T.writes(Y[vi, vj])
                    Y[vi, vj] = Y[vi, vj] + A[vi, vk] * B[vk, vj]
            for ax0 in T.serial(4):
                with T.block("C"):
                    vi = T.axis.spatial(128, i)
                    vj = T.axis.spatial(128, j_0 * 4 + ax0)
                    T.reads(Y[vi, vj])
                    T.writes(C[vi, vj])
                    C[vi, vj] = T.max(Y[vi, vj], T.float32(0))

对应的 Low-level Numpy 函数如下

def lnumpy_mm_relu_v3(A: np.ndarray, B: np.ndarray, C: np.ndarray):
    Y = np.empty((128, 128), dtype="float32")
    for i in range(128):
        for j0 in range(32):
            # Y_init
            for j1 in range(4):
                j = j0 * 4 + j1 
                Y[i, j] = 0
            # Y_update
            for k in range(128):
                for j1 in range(4):
                    j = j0 * 4 + j1 
                    Y[i, j] = Y[i, j] + A[i, k] * B[k, j]
            # C
            for j1 in range(4):
                j = j0 * 4 + j1 
                C[i, j] = max(Y[i, j], 0)

Why Do Loop Influence the Exec Time

CPU Architecture
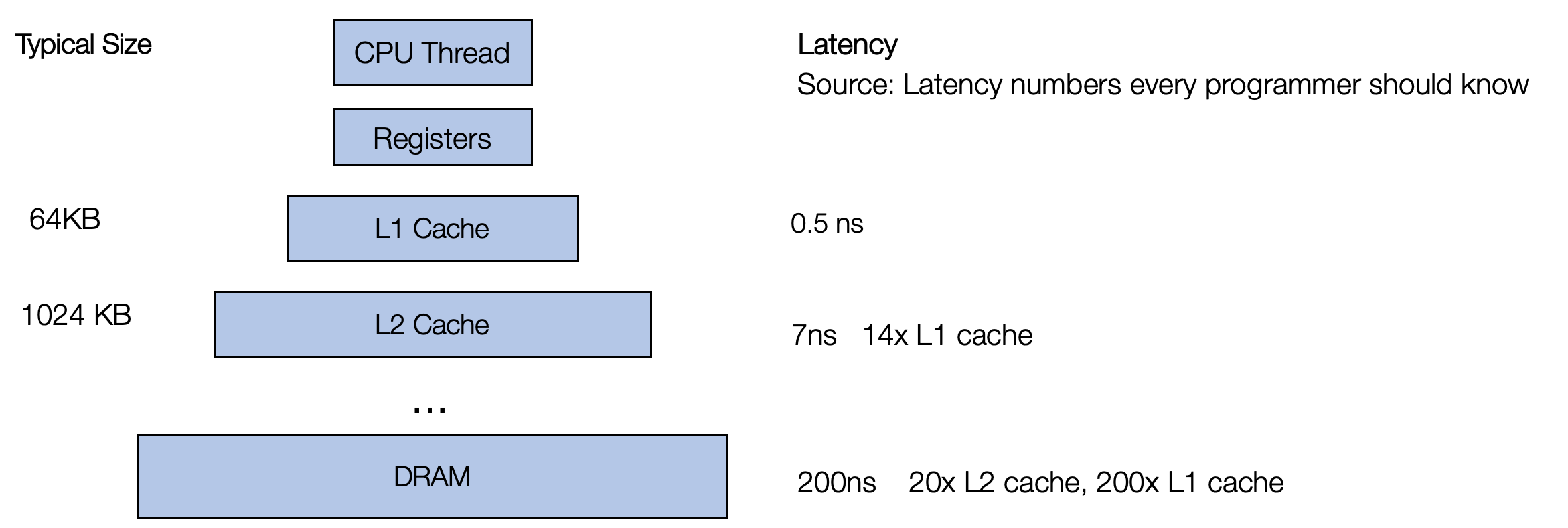
CPU 带有多级缓存，需要先将数据提取到缓存中，然后 CPU 才能访问它。而且访问已经在缓存中的数据要快得多。CPU 采用的一种策略是获取彼此更接近的数据。当我们读取内存中的一个元素时，它会尝试将附近的元素（Cache Line）获取到缓存中，当读取下一个元素时它已经在缓存中。因此，具有连续内存访问的代码通常比随机访问内存不同部分的代码更快。

Loop Order
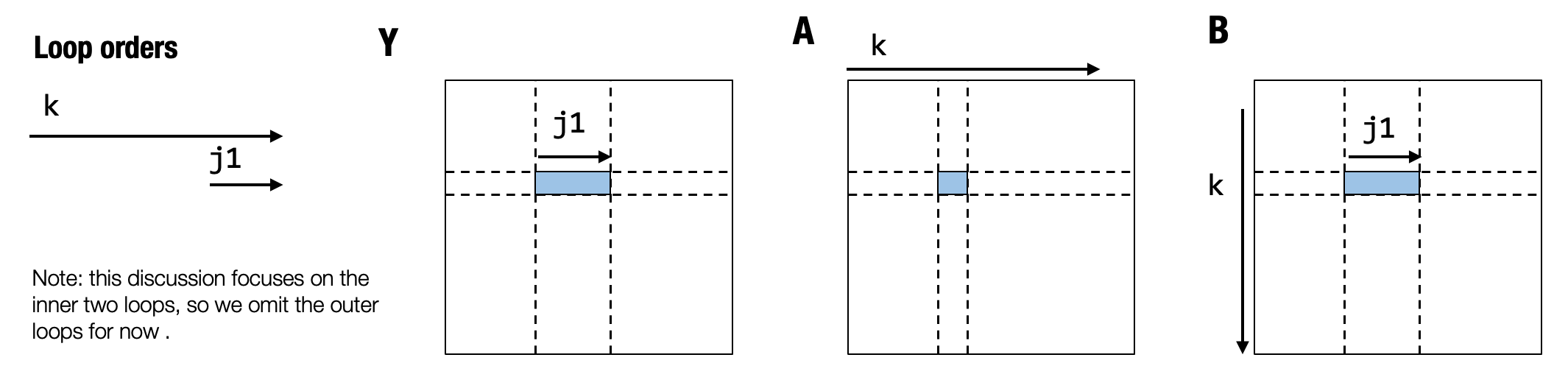
j1 这一迭代产生了对 B 元素的连续访问。具体来说，它意味着在 j1=0 和 j1=1 时我们读取的值彼此相邻。这可以让我们拥有更好的缓存访问行为。此外，我们使 C 的计算更接近 Y，从而实现更好的缓存行为。

Ways to Create and Interact with TensorIR

Create TensorIR via TVMScript

创建 TensorIR 函数的第一种方法是直接在 TVMScript 中编写函数，它也是一种在变换过程中检查张量函数的有用方法。我们可以打印出 TVMScript，进行一些手动编辑，然后将其反馈给 MLC 流程以调试和尝试可能的（手动）变换，然后将变换后的程序重新应用到 MLC 流程中。

Generate TensorIR code using Tensor Expression

张量表达式 (TE) 是一种特定领域的语言，它通过 API 之类的表达式描述一系列计算。MM-ReLU 可以通过以下程序完成

from tvm import te
A = te.placeholder((128, 128), "float32", name="A")
B = te.placeholder((128, 128), "float32", name="B")
k = te.reduce_axis((0, 128), "k")
Y = te.compute((128, 128), lambda i, j: te.sum(A[i, k] * B[k, j], axis=k), name="Y")
C = te.compute((128, 128), lambda i, j: te.max(Y[i, j], 0), name="C")

TVM

#TVM learning

TVM Learning (2)-Tensor Program Abstraction Case Study-TensorIR

https://darkenstar.github.io/2024/08/15/chapter2/

Author

ANNIHILATE_RAY

Posted on

August 15, 2024

Licensed under

TVM Learning (3)-Schedule Analysis Previous

TVM Learning (1)-Tensor Program Abstraction in Action Next